چارچوب مرجع لخت
مکان یا هر سرعت هر جسم فقط نسبت به اجسام دیگر معنی پیدا می کند. چارچوب مرجع نیز یک موجود فیزیکی است (مانند جاده، قطار، درخت و یا خود کره ی زمین) که دستگاه مختصات به آن متصل شده است. چارچوب مرجعی که در آن قانون اول نیوتون صادق باشد، چهارچوب مرجع لخت نامیده می شود. چنین چارچوب هایی با استفاده از قانون اول نیوتون ...
نیرو
اکنون ما باید یکای نیرو را تعریف کنیم. ما می دانیم که نیرو می تواند به یک جسم شتاب بدهد، بنابراین ما باید یکای نیرو را برحسب شتاب داده شده به جسم استاندارد تعریف کنیم. هنگامی که نیرویی به جسمی به جرم یک کیلوگرم شتابی برابر با یک متر بر مجذور ثانیه می دهد بزرگی این نیرو برلابر یا یک نیوتون است و هنگامی که دو برابر نیروی بالا را ...
مکانیک نیوتونی
رابطه ی بین نیرو و شتاب اولین بار توسط آیزاک نیوتون (1727- 1642) مطرح شد. تدوین قوانین کلاسیک حرکت، از جمله قانون دوم نیوتون که قانون اساسی دینامیک محسوب می شود، از کارهای وی محسوب می شود. در اوایل قرن بیستم با ظهور دو نظریه ی نسبیت خاص و مکانیک کوانتومی معلوم شد که مکانیک کلاسیک (نیوتونی) در مورد سرعت های خیلی زیاد ( نزدیک ...
حرکت دایره ای یکنواخت
هنگامی که ذره ای با تندی ثابت در یک مسیر دایره ای به شعاع r حرکت می کند، (شکل 4-6.) جهت بردار سرعت، پیوسته تغییر می کند که این تغییر جهت بردار سرعت باعث ایجاد شتاب می شود. ما می توانیم بردار سرعت را به صورت زیر بنویسیم:
(30-4)
با توجه به شکل 4-7 با جایگزین کردن مقادیر sinθ با yp/r و cosθ با xp/r داریم:
(31-4)
با مشتق گرفتن ...
معادله ی مسیر حرکت پرتابه
با حذف t بین معادلات حرکت در راستای افقی (4-21) و حرکت در راستای قائم (4-22)، معادله ی مسیر حرکت پرتابه بدست می آید:
(25-4)
برد پرتابه
برای پیدا کردن برد یا بیشترین مسافت افقی طی شده، ابتدا زمان پرواز را از معادله ی زیر بر حسب R تعیین می کنیم:
(26-4)
هنگلامی که پرتابه به زمین برخورد می کند y در معادله ی 4-22 صفر می ...
شتاب متوسط و لحظه ای
زمانی که سرعت ذره در بازه زمانی Δtتغییر می کند، شتاب متوسط ذره در این بازه ی زمانی برابر است با:
(13-4)
و شتاب لحظه ای برابر است با:
(14-4)
با استفاده از معادله ی بدستن آمده برای سرعت (معادله ی 4-12) می توانیم بنویسیم:
(15-4)
(16-4)
که در آن:
(17-4)
حرکت پرتابه ها
هنگامی که پرتابه ای با سرعت اولیه v0 پرتاب می شود داریم ...
سرعت متوسط و لحظه ای
در اینجا نیز مانند حالت یک بعدی، سرعت متوسط برابر است با نسبت جابه جایی به مدت سپری شده:
(7-4)
با استفاده از معادله ی 4-6، خواهیم داشت:
(8-4)
و سرعت لحظه ای برابر است با مشتق مکان نسبت به زمان:
(9-4)
(10-4)
(11-4)
که در آن:
(12-4)
...
حرکت در دو و سه بعد
یک روش کلی برای تعیین مکان ذره در فضا استفاده از بردار مکان است. برداری که معمولا از یک نقطه ی مرجع (مبدا مختصات) به طرف مکان ذره کشیده می شود. در فضای سه بعدی، بردار مکان ذره ای با مختصات x ، y و z را به صورت زیر نمایش می دهیم:
(1-4)
برای مثال بردار مکان ذره ی نشان داده شده در شکل 4-1 به شکل زیر داده می می ...
ضرب برداری
ضرب برداری بردارهای a و b که با a⨯b نشان داده می شود یک بردار سوم c تولید می کند که بزرگی آن برابر است با:
(22-3)
در این جا ϕ زاویه ی بین دو بردار است. (ما باید کوچکترین زاویه ی بین برداها را درنظر بگیریم چون sin ϕ وsin (360˚–ϕ) علامت جبری متفاوتی دارند.
"اگر بردارهای a و b موازی یا پاد موازی باشند، حاصل ضرب برداری آن ها صفر است. ...
ضرب بردارها
سه راه برای ضرب بردارها وجود دارد، که دقیقا شبیه به عمل ضرب در جبر معمولی نیست.
ضرب یک اسکالر در بردار
اگر ما یک اسکالر s را در یک بردار a ضرب کنیم، یک بردار جدید خواهیم داشت. بزرگی آن برابر است با حاصل ضرب بزرگی a و قدر مطلق s. جهت آن در جهت بردار a است اگر s مثبت باشد و اگر s منفی باشد بردار حاصل در خلاف جهت بردار a خواهد بود. ...
بردارهای یکه
یک بردار یکه برداری است با بزرگی دقیقا برابر با 1 و یک جهت مشخص. همچنین بردار یکه بدون بعد و یکاست. بردارهای یکه در جهت مثبت محورهای x، y و zدر شکل3-9 نشان داده شده است. آرایش محورها در شکل3-9، دستگاه مختصات راستگرد (دست راستی) نامیده می شود.
بردارهای یکه، برای بیان بردارها بسیار مفید هستند. برای مثال، ما می توانیم بردارهای a ...
مولفه های بردارها
جمع بردارها به روش هندسی می تواند خسته کننده باشد. یک روش تمیز و آسانتر شامل جبری وجود دارد، اما در این روش ما نیاز داریم که بردار را در یک دستگاه مختصات راست گوشه قرار دهیم. محورهای x وy همانند شکل 3-7، معمولا در یک صفحه ی کشیده می شود. و محور z از مبدا مستقیم به طرف خارج صفحه قرار می گیرد، و در حالت دو بعدی از آن چشم ...
جمع بردارها
فرض کنید که در نمودار برداری شکل 3-2، یک ذره از A به B و سپس ازB به C حرکت می کند. ما می توانیم این جابه جایی را با دو بردار جابه جایی AB و BC نشان دهیم. جابه جایی خالص ناشی از این دو بردار، یک جابه جایی از A به C است. ما AC را بردار حاصل جمع یا بردار برآیند بردارهای AB و BC می نامیم. یک روش برای نشان دادن بردارها، استفاده از حروف و قرار ...
بردارها و اسکالرها
یک ذره که در طول یک خط راست حرکت می کند فقط می تواند در دو جهت حرکت کند. ما می توانیم حرکت آن را در یک جهت مثبت و در جهت دیگر منفی درنظر بگیریم. برای ذراتی که در سه بعد حرکت می کنند، یک علامت منفی و یک علامت مثبت برای تعیین جهت حرکت کافی نیست. بنابراین باید از بردار استفاده کنیم.
یک بردار دارای جهت و بزرگی است، و از ...
استفاده از انتگرال و مساحت
در بخش های قبل دیدیم که چگونه می توان سرعت را از نمودار مکان- زمان و شتاب را از نمودار سرعت- زمان تعیین کرد. در این بخش ما با استفاده از انتگرال و مساحت زیر نمودارها به محاسبه تغییر مکان و تغییر سرعت می پردازیم.
با توجه به رابطه بدست آمده برای شتاب، داریم:
(15-2)
و مقدار این انتگرال برابر است با مساحت سطح ...




 فارسی ساز Sleeping Dogs
فارسی ساز Sleeping Dogs فارسی ساز Watch Dogs
فارسی ساز Watch Dogs آموزش جامع افزایش امنیت و ضد هک کردن وای فای
آموزش جامع افزایش امنیت و ضد هک کردن وای فای فارسی ساز Watch Dogs 2 نسخه PS4
فارسی ساز Watch Dogs 2 نسخه PS4 دانلود کتاب صوتی فوق العاده نیک سرشت
دانلود کتاب صوتی فوق العاده نیک سرشت پیش خرید فارسی ساز Watch Dogs
پیش خرید فارسی ساز Watch Dogs فول ست کردی2025 ارگ اندروید
فول ست کردی2025 ارگ اندروید دانلود فایلهای بسته آمادهچاپ و نصب تابلو اعلانات مسجدنما هفته چهارم فروردین ماه 1404
دانلود فایلهای بسته آمادهچاپ و نصب تابلو اعلانات مسجدنما هفته چهارم فروردین ماه 1404 دانلود فایل بسته آمادهچاپ و نصب تابلو اعلانات مسجدنما اردیبهشت ماه 1404
دانلود فایل بسته آمادهچاپ و نصب تابلو اعلانات مسجدنما اردیبهشت ماه 1404 پیک نوروزی ریاضی پنجم دانیال گنجی
پیک نوروزی ریاضی پنجم دانیال گنجی احمد وزیر
احمد وزیر دانلود فایل بسته آمادهچاپ و نصب تابلو اعلانات مسجدنما هفته پنجم اردیبهشت ماه 1404
دانلود فایل بسته آمادهچاپ و نصب تابلو اعلانات مسجدنما هفته پنجم اردیبهشت ماه 1404 دانلود فایل بسته آمادهچاپ و نصب تابلو اعلانات مسجدنما هفته دوم اردیبهشت ماه 1404
دانلود فایل بسته آمادهچاپ و نصب تابلو اعلانات مسجدنما هفته دوم اردیبهشت ماه 1404 دانلود فایلهای بسته آمادهچاپ و نصب تابلو اعلانات مسجدنما هفته سوم فروردین ماه 1404
دانلود فایلهای بسته آمادهچاپ و نصب تابلو اعلانات مسجدنما هفته سوم فروردین ماه 1404 کتاب حل المسائل شیمی عمومی سیلبربرگ
کتاب حل المسائل شیمی عمومی سیلبربرگ پاورپوینت از گذشته تا آینده نان درس 14 علوم دوم
پاورپوینت از گذشته تا آینده نان درس 14 علوم دوم پاورپوینت درس پنجم اندیشه اسلامی(1) صفات خدا
پاورپوینت درس پنجم اندیشه اسلامی(1) صفات خدا پاورپوینت درس 13 علوم تجربی پایه سوم دبستان (ابتدایی): هر کدام جاي خود (2)
پاورپوینت درس 13 علوم تجربی پایه سوم دبستان (ابتدایی): هر کدام جاي خود (2) سوالات نهاد تاریخ تحلیلی صدر اسلام مبحث نگاه تاریخی به دین مسیحیت همراه با پاسخ
سوالات نهاد تاریخ تحلیلی صدر اسلام مبحث نگاه تاریخی به دین مسیحیت همراه با پاسخ پاورپوینت الدرس السادس (آنّه ماري شيمِل، تَرجَمَةُ الْفِعْلِ الْمُضارِعِ 2) درس 6 عربی یازدهم ریاضی و تجربی
پاورپوینت الدرس السادس (آنّه ماري شيمِل، تَرجَمَةُ الْفِعْلِ الْمُضارِعِ 2) درس 6 عربی یازدهم ریاضی و تجربی کتاب راهنمای سلامت انسان از هری بی جوزف pdf
کتاب راهنمای سلامت انسان از هری بی جوزف pdf پاورپوینت درس پنجم تاریخ تحلیلی صدر اسلام از هجرت مسلمانان به حبشه تا هجرت به یثرب
پاورپوینت درس پنجم تاریخ تحلیلی صدر اسلام از هجرت مسلمانان به حبشه تا هجرت به یثرب![دانلود جزوه خلاصه [انسان شناسی فرهنگی] - دانیل بیتس، فرد بلاگ - محسن ثلاثی- پیام نور -با دو فرمت word و pdf](https://4kia.ir/s4/img_project/45738_1661005841.jpg) دانلود جزوه خلاصه [انسان شناسی فرهنگی] - دانیل بیتس، فرد بلاگ - محسن ثلاثی- پیام نور -با دو فرمت word و pdf
دانلود جزوه خلاصه [انسان شناسی فرهنگی] - دانیل بیتس، فرد بلاگ - محسن ثلاثی- پیام نور -با دو فرمت word و pdf آدمی یک تاریخ نوید بخش.pdf
آدمی یک تاریخ نوید بخش.pdf دانلود کتاب صوتی فوق العاده موهبت شگفت انگیز خشم
دانلود کتاب صوتی فوق العاده موهبت شگفت انگیز خشم پاورپوینت درس 11 آمادگی دفاعی پایه دهم (دروس مشترک): پدافند غیرعامل (ویرایش 1403)
پاورپوینت درس 11 آمادگی دفاعی پایه دهم (دروس مشترک): پدافند غیرعامل (ویرایش 1403) پاورپوینت درس 30 تفکر و سبک زندگی پایه هشتم: ارزش ها و معیارهای رفتاری
پاورپوینت درس 30 تفکر و سبک زندگی پایه هشتم: ارزش ها و معیارهای رفتاری پاورپوینت راه خوشبختی درس 17 فارسی هشتم
پاورپوینت راه خوشبختی درس 17 فارسی هشتم پاورپوینت درس سبک زندگی چیست و عوامل موثر بر آن کدام است تفکر و سبک زندگی هفتم
پاورپوینت درس سبک زندگی چیست و عوامل موثر بر آن کدام است تفکر و سبک زندگی هفتم فروش فیلتر بورسی استریکلی فقط 75 هزار تومان
فروش فیلتر بورسی استریکلی فقط 75 هزار تومان کسب درآمد اینترنتی 300000 تومان در خانه در کمتر از 30 دقیقه
کسب درآمد اینترنتی 300000 تومان در خانه در کمتر از 30 دقیقه روش درآمدزایی در خواب (تعجب نکنید! کلیک کنید و بخوانید)
روش درآمدزایی در خواب (تعجب نکنید! کلیک کنید و بخوانید) کسب و کار اینترنتی با درآمد میلیونی
کسب و کار اینترنتی با درآمد میلیونی ربات همه کاره اینستاگرام
ربات همه کاره اینستاگرام كسب درآمد اينترنتي روزانه حداقل100هزار تومان تضميني
كسب درآمد اينترنتي روزانه حداقل100هزار تومان تضميني کسب درآمد ابدی و بی نهایت 100% واقعی
کسب درآمد ابدی و بی نهایت 100% واقعی کسب درآمد روزانه حداقل یک میلیون تومان ! کاملا حلال و واقعـی !!
کسب درآمد روزانه حداقل یک میلیون تومان ! کاملا حلال و واقعـی !! مجموعه ی آموزش تعمیر لامپ کم مصرف (از مبتدی تا پیشرفته)
مجموعه ی آموزش تعمیر لامپ کم مصرف (از مبتدی تا پیشرفته) افزایش ممبر کانال، گروه و ربات تلگرام به صورت بی نهایت (اد ممبر)
افزایش ممبر کانال، گروه و ربات تلگرام به صورت بی نهایت (اد ممبر) دانلود مجموعه آموزشی پایپینگ ( Piping ) و نقشه خوانی + آموزش سه نرم افزار طراحی و تحلیل لوله کشی صنعتی
دانلود مجموعه آموزشی پایپینگ ( Piping ) و نقشه خوانی + آموزش سه نرم افزار طراحی و تحلیل لوله کشی صنعتی آموزش بازكردن انواع قفل ها بدون كليد(ويژه)
آموزش بازكردن انواع قفل ها بدون كليد(ويژه) آموزش برنامه نویسی آردوینو
آموزش برنامه نویسی آردوینو کسب و کار اینترنتی در منزل
کسب و کار اینترنتی در منزل بازگردانی پیامک های حذف شده- ریکاوری پیامک ۱۰۰٪ عملی
بازگردانی پیامک های حذف شده- ریکاوری پیامک ۱۰۰٪ عملی آموزش رایگان کسب درآمد از سایت الیمپ ترید ( olymp trade )
آموزش رایگان کسب درآمد از سایت الیمپ ترید ( olymp trade ) اموزش ویرایش امضا و پکیج برنامه اندروید و کسب درامد از مارکت های اندرویدی
اموزش ویرایش امضا و پکیج برنامه اندروید و کسب درامد از مارکت های اندرویدی دانلود نمونه فاکتور آماده با فرمت ورد - اکسل و عکس
دانلود نمونه فاکتور آماده با فرمت ورد - اکسل و عکس آموزش ساخت بازی بدون دانش برنامه نویسی و طراحی سه بعدی مبتدی تا پیشرفته با نرم افزار
آموزش ساخت بازی بدون دانش برنامه نویسی و طراحی سه بعدی مبتدی تا پیشرفته با نرم افزار کد های آماده html و css جهت یادگیری و طراحی سریع
کد های آماده html و css جهت یادگیری و طراحی سریع اموزش کسب درامد از اینترنت روزانه ۳میلیون تومان تضمینی و تست شده 1403
اموزش کسب درامد از اینترنت روزانه ۳میلیون تومان تضمینی و تست شده 1403 آموزش كامل تعمير لامپ كم مصرف(اختصاصي)
آموزش كامل تعمير لامپ كم مصرف(اختصاصي) نسخه خطی اشعار و پیشگویی های شاه نعمت الله ولی
نسخه خطی اشعار و پیشگویی های شاه نعمت الله ولی نسخه خطی اشعار و پیشگویی های شاه نعمت الله ولی
نسخه خطی اشعار و پیشگویی های شاه نعمت الله ولی درامدزایی در خواب! (تعجب نکنید! بخوانید)
درامدزایی در خواب! (تعجب نکنید! بخوانید) مدار داخلی واکی تاکی(اموزش ساخت)
مدار داخلی واکی تاکی(اموزش ساخت) کتاب افزایش ممبر کانال تلگرام
کتاب افزایش ممبر کانال تلگرام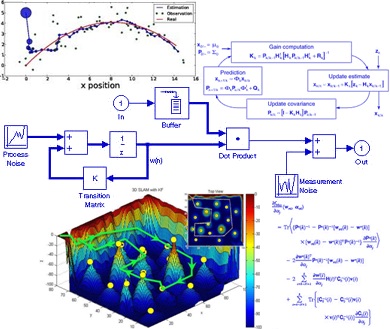 دانلود پاورپوینت فیلتر کالمن بر روی یک سنسور شتاب سنج برای تخمین سه متغیر حالت
دانلود پاورپوینت فیلتر کالمن بر روی یک سنسور شتاب سنج برای تخمین سه متغیر حالت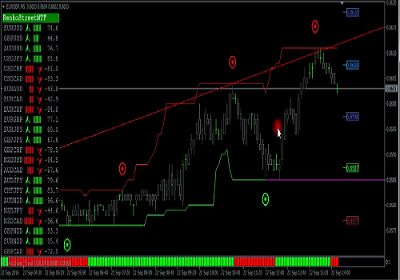 اندیکاتور ای کیو آپشن
اندیکاتور ای کیو آپشن